논문 링크: https://arxiv.org/abs/1811.10959
깃허브 링크: https://github.com/SsnL/dataset-distillation
1. Introduction
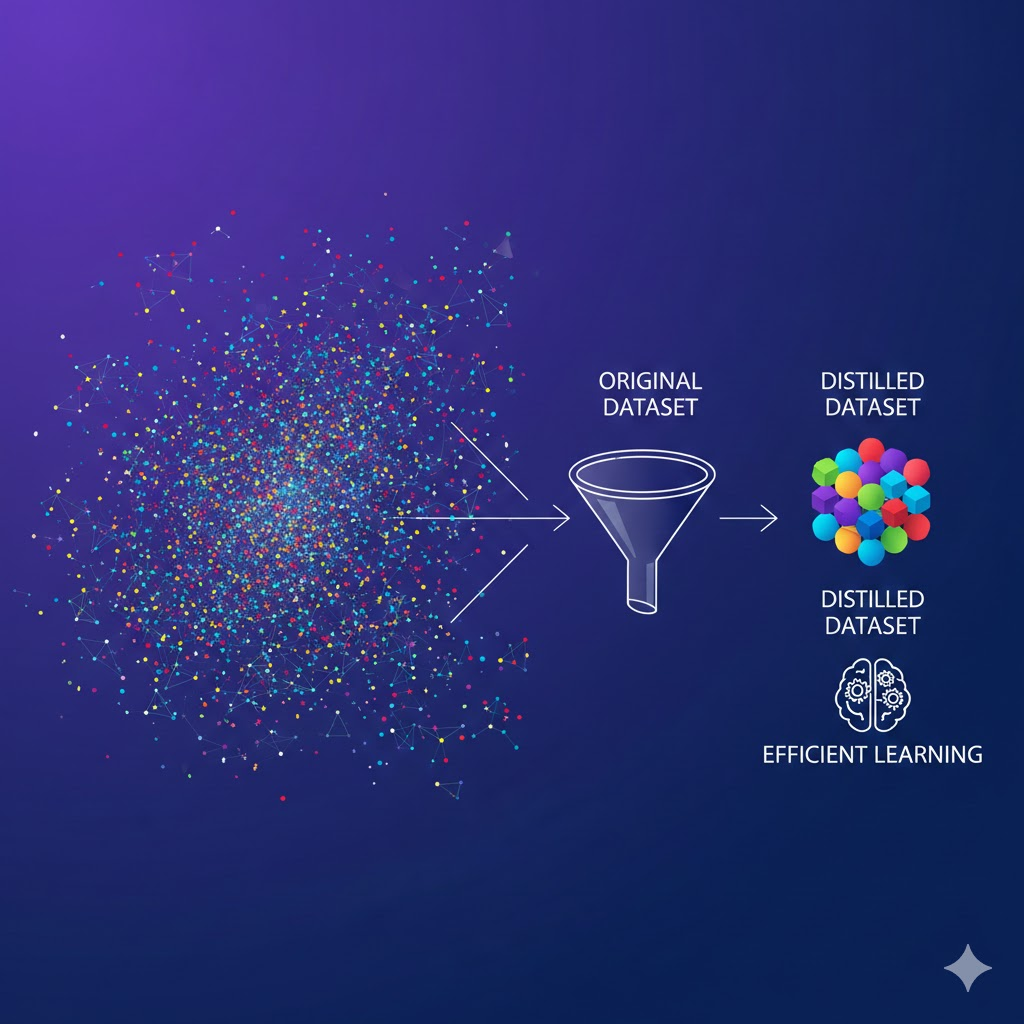
본 논문은 Dataset Distillation에 대한 개념을 처음으로 제안한 논문입니다.
Dataset Distillation이란 무엇일까?
Dataset Distillation이란 대규모의 real images를 소수의 synthetic images로 압축하여, synthetic images만으로 어떤 모델을 학습시켰을 때 real images로 학습한 것과 유사한 성능을 달성하게 만드는 기법이라고 할 수 있습니다.

논문에서 제시한 사진을 보면 dataset distillation에 대해 대충 감이 잡힐 것입니다.
본 논문에서는 image classification 태스크에 대해 dataset distillation을 수행하고, 매우 흔하게 사용되는 두 가지 벤치마크 데이터셋인 MNIST와 CIFAR10을 활용하여 성능을 평가합니다.
본 논문의 contribution을 요약하면 다음과 같습니다.
- 원본 데이터의 정보를 압축하여 몇 번의 GD step만으로 모델을 빠르게 학습시킬 수 있는 distilled images 생성 방법론, 즉 dataset distillation을 제안함. 알고리즘은 모델 weight 대신 distilled images 픽셀 값을 최적화하는 방식으로 동작함.
- 다양한 방식으로 초기화된 모델에도 일반화되는 방법, 여러 step과 epoch를 통한 성능 향상 기법, distilled images 개수의 하한에 대한 분석을 제시함.
- Distilled images를 활용한 pre-trained 모델에 대한 fine-tuning, malicious dataset poisoning attack에 대한 실험 결과도 보고함.
2. Related Works
Knowledge Distillation

원래 knowledge distillation 기법이 teacher model의 지식을 student model에게 증류하는 데 사용되었다면, dataset distillation은 대규모의 이미지의 지식을 압축하는 데 사용되었다고 생각하면 되겠습니다.
- Knowledge Distillation: 복잡한 모델(teacher) → 간단한 모델(student)로 지식 전달
- Dataset Distillation: 대규모 데이터셋 → 소수의 합성 이미지로 지식 압축
Dataset pruning, core-set construction, and instance selection

기존에도 original dataset에서 valuable한 데이터들만 모아 small subset을 구성하는 다양한 연구가 수행되었다고 합니다.
하지만 이런 방식들은 카테고리별로 (본 논문보다) 상대적으로 더 많은 데이터 샘플을 필요로 한다-라고 하며 본 논문의 필요성을 강조하고 있습니다.
Gradient-based hyperparameter optimization

정의: hyperparameter가 최종 성능에 미치는 영향을 gradient로 계산하여 모델 weight 뿐만 아니라 hyperparameter까지 함께 최적화하는 기법으로, 기존 연구들은 보통 validation loss에 대해서 gradient를 계산한다고 합니다.
이와 유사하게 dataset distillation은 optimization 과정을 기반으로 동작하지만, distilled images 생성에 더 초점을 맞춥니다.
또한 random initialized 모델에 대해서 더 잘 작동하게 만들었는데, 이는 이전 연구들에서는 불가능했다고 합니다.
Understanding datasets

기존 연구들에서는 학습된 모델을 이해하고 그에 대한 정보를 시각화하는 연구가 많이 진행되었다고 합니다.
본 논문에서는 모델보다는 "데이터셋"에 더 집중하는 쪽으로 연구 방향을 잡은 것으로 이해하면 되겠습니다.
3. Warm-up
Approach 부분이 6가지 섹션으로 나뉘어져 있는데, 적절히 나눠서 설명해 보겠습니다.
수식이 많지만 그렇게 어렵진 않습니다. 시작해보죠.. 😊
목표: 어떤 모델과 데이터셋이 주어졌을 때, 원본 데이터셋과 거의 동등한 성능을 내는 distilled images를 얻는 것.

- x: training dataset
- θ: model weight
- l: loss function (여기선 2번 미분 가능하다고 가정함)

- x_t: minibatch
보통 일반적인 GD에서는 각 스텝에서 x_t를 사용해서 오직 모델의 파라미터 θ 만 업데이트하죠.
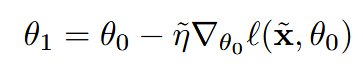
- x ̃: distilled images
- η ̃: learning rate for dataset distillation
Dataset distillation 과정에서는 모델의 파라미터 θ를 업데이트하는 것이 아닙니다.
θ_0 은 고정시킨 상태로.. 우리가 생성한 distilled images와 learning rate 가지고 모델의 파라미터를 딱 한 번만 업데이트합니다.
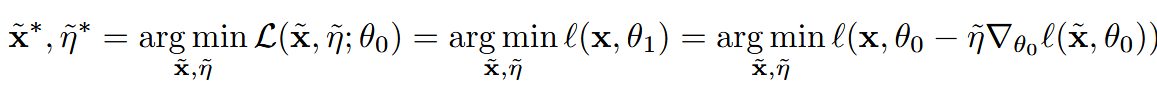
Equation2로 new weight θ_1을 얻게 되고, 그 후 real image x를 new weight 모델에 통과시켜서 loss를 계산합니다.
그 후 θ_1을 기반으로 loss를 계산하여 x ̃와 η ̃를 업데이트하는 것이 기본 아이디어입니다.
수식처럼 θ_1이 x ̃와 η ̃에 대해 미분 가능한 형태로 표현되므로, loss를 기반으로 gradient-based optimization이 가능하게 됩니다.

하지만 여기서 짚고 가야 할 문제점이 있습니다.
특정 θ_0 하나에 대해서만 distilled images를 만들게 되면, 이미지 안에 θ_0의 정보가 같이 인코딩됩니다.
즉, 다른 값으로 초기화된 모델에서는 잘 작동하지 않아 일반화된 distilled images를 얻기 어렵게 되죠.
이를 해결하기 위해 논문에서는 같은 분포(Xavier 초기화)에서 여러 가중치를 샘플링한 후, 이들에 대한 평균 손실을 최소화하도록 distilled images를 최적화하는 방법을 제안합니다.
예를 들면 같은 구조(예: LeNet)인데 초기 가중치만 다른 4개의 네트워크를 두고 최적화를 진행하는 거죠.
- 네트워크 1: θ₀⁽¹⁾ = [0.12, -0.34, ...]
- 네트워크 2: θ₀⁽²⁾ = [-0.21, 0.15, ...]
- 네트워크 3: θ₀⁽³⁾ = [0.08, 0.29, ...]
- 네트워크 4: θ₀⁽⁴⁾ = [-0.05, -0.18, ...]
4. Main Algorithm

자, 이제 그래서 본 논문의 핵심인 distilled images를 어떻게 만드는가에 대해 알아보겠습니다.








앞서 설명한 것처럼, dataset distillation에서는 모델 파라미터 θ를 학습하는 것이 아닙니다.
θ₀를 고정한 채로 증류 데이터 x̃와 학습률 η̃로 한 스텝만 업데이트하여 θ₁을 얻고, 이 θ₁이 실제 데이터에서 낮은 손실을 가지도록 x̃와 η̃를 역전파로 최적화하는 것이 핵심입니다.
다음과 같이 정리할 수 있습니다.
"랜덤하게 초기화된 모델이 있을 때, 좋은 데이터가 있다면 단 한 스텝만 학습해도 손실이 크게 줄어든다.
이 관계를 역으로 이용해서, 손실을 가장 많이 줄이는 방향으로 데이터 자체를 최적화하자."

증류 데이터로 한 스텝 업데이트된 모델이 실제로 잘 학습되었는지 평가하는 단계입니다.
실제 학습 데이터 xₜ를 θ₁⁽ʲ⁾에 통과시켜 손실 L⁽ʲ⁾를 계산하여, 이 loss가 낮을수록 증류 데이터가 효과적이라는 의미이므로 이 값을 기준으로 x̃와 η̃를 최적화합니다.


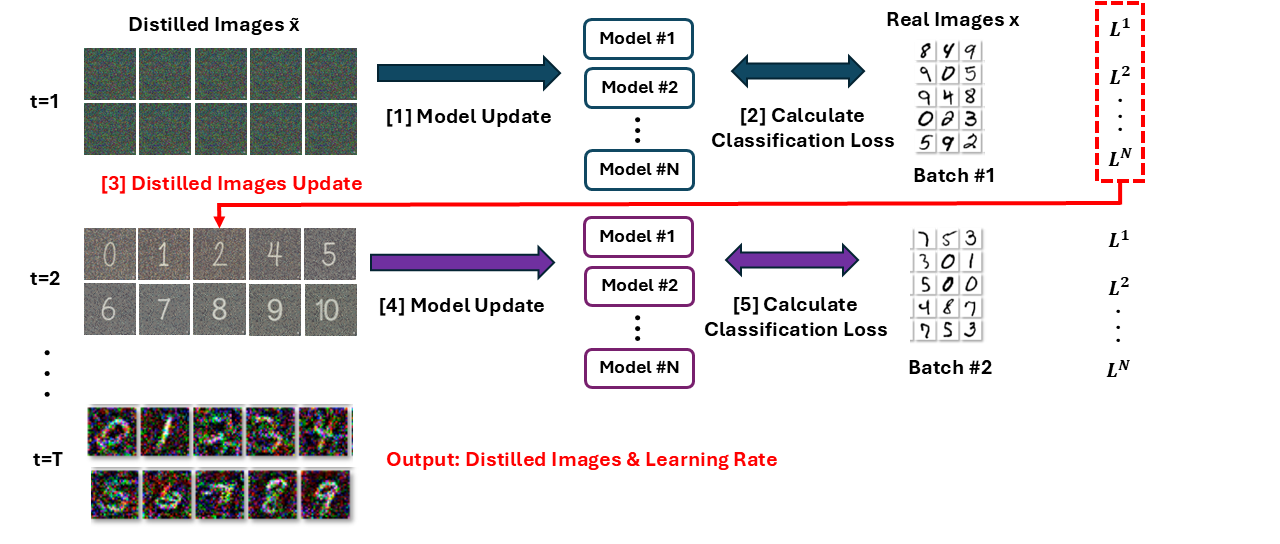
이 모든 과정을 그림으로 요약하면 위와 같이 정리할 수 있겠습니다. (자료 열심히 만들어봤는데..! 이해가 잘 되셨길 바랍니다.😊)
지금까지 Algorithm 1의 기본 동작을 살펴보았습니다.
이어서 이론적 분석과 함께 성능을 더욱 향상하기 위한 확장 방법들을 알아보겠습니다.
5. Theoretical Analysis & Extensions
이번에는 3.3 Analysis of A Simple Linear Case, 3.4 Multiple Gradient Descent Steps and Multiple Epochs, 3.5 Distillation with Different Initializations 섹션을 설명해보겠습니다.
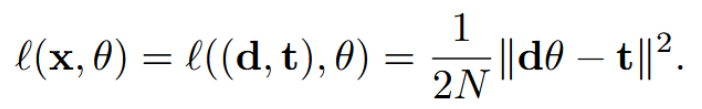
- x = (d, t): 데이터. d는 입력(N×D 행렬), t는 타겟(N×1 벡터)
- θ: 모델 파라미터(D×1 벡터)
- dθ: 모델의 예측값
- ||dθ - t||²: 예측값과 타겟 간의 차이(MSE)
논문에서는 복잡한 신경망 대신 단순한 선형 모델을 사용하여 증류 데이터가 최소 몇 개 필요한지에 대한 이론적 하한을 도출합니다.

위의 Eq.6을 distilled images 상황에 대입하면 분모가 N -> M이 됩니다.
그리고 ℓ(x̃, θ₀)을 미분한다고 하면 노란색 항이 되겠지요.
마지막 항은 그저 세 번째 항을 θ₀ 에 대해 정리한 항이 되겠습니다.
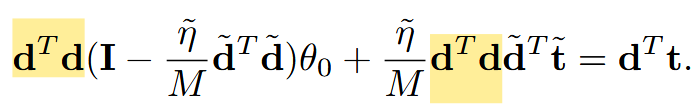
선형 회귀에서 전역 최솟값(global minimum)의 조건은 dᵀdθ* = dᵀt입니다.
θ₁이 전역 최솟값이 되려면 이 조건을 만족해야 하므로 dᵀdθ₁ = dᵀt가 성립해야 합니다.
잘 보면 어렵지 않습니다.
앞서 유도한 Eq.7을 θ₁ 자리에 넣어준 것이 전부입니다.
곱해진 dᵀd 이것만 노란색으로 표시했습니다!
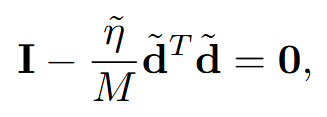
θ₀는 랜덤 초기화이므로 어떤 값이든 될 수 있습니다.
만약 θ₀에 곱해지는 부분이 0이 아니면, θ₀ 값에 따라 좌변이 달라지므로 모든 θ₀에서 등식이 성립할 수 없게 되죠.
따라서 θ₀에 곱해지는 부분인 I - (η̃/M)d̃ᵀd̃가 0이 되어야 합니다.
이 조건이 성립하려면 d̃ᵀd̃가 항등행렬 I와 같아져야 합니다.
여기서 I는 D×D 항등행렬이고, d̃ᵀd̃도 D×D 행렬입니다.
d̃ᵀd̃가 I와 같아지려면 full rank(rank D)여야 하는데, d̃는 M×D 행렬이므로 d̃ᵀd̃의 rank는 최대 min(M, D)입니다.
따라서 full rank가 되려면 M ≥ D라는 조건이 필요하게 되는 거죠.
즉, 증류 데이터의 개수 M은 최소한 데이터 차원 D 이상이어야 어떤 초기화에서든 전역 최솟값에 도달할 수 있다는 결론이 나옵니다.
[Discussion]
M ≥ D 조건은 증류 데이터가 최소 데이터 차원만큼 필요하다는 뜻입니다.
예를 들어 MNIST는 784차원, CIFAR10은 3072차원이므로 수백~수천 장의 증류 이미지가 필요해져 압축의 의미가 없어지게 되는 거죠.
이러한 한계로 인해 논문에서는 "모든 θ₀"에 일반화하는 것을 포기하고, 비슷한 지역적 조건을 가지는 특정 초기화 분포 p(θ₀)에 집중합니다 (Section 3.5).
또한 single step의 한계를 극복하기 위해 여러 GD 스텝으로 확장합니다 (Section 3.4).

[Multiple GD Steps]
기존 Algorithm 1의 Line 6에서는 update를 한 스텝만 수행했지요.
이를 여러 스텝으로 확장하여 각 스텝마다 다른 증류 데이터 배치 x̃ᵢ와 학습률 η̃ᵢ를 사용하도록 변경합니다.
앞서 소개드린 과정에서는 (Line 6) 증류 데이터 x̃ 하나로 한 번만 업데이트 & 학습률 η̃ 하나만 최적화하죠.
확장 버전에서는 다음과 같이 학습을 수행합니다.
- Line 6: 여러 증류 데이터 x̃₀, x̃₁, ..., x̃₉로 순차적으로 10번 업데이트
- 학습률 η̃₀, η̃₁, ..., η̃₉ 각각 최적화
- 에포크 반복 시 같은 이미지 재사용, 학습률은 에포크마다 따로 최적화
- Line 9: 모든 스텝을 통해 역전파
+ 여러 스텝을 역전파하면 메모리와 계산 비용이 많이 들기 때문에, back-gradient optimization 기법을 사용하여 효율적으로 gradient를 계산했다고 하네요.
[Multiple Epochs]
Multiple epochs는 이미 만들어진 증류 데이터로 모델을 학습시킬 때, 같은 이미지 시퀀스를 여러 번 반복 사용한다는 얘기입니다.
[Different Initializations]
바로 위에서 모든 θ₀에 일반화하려면 M ≥ D가 필요하다는 것을 수식을 통해 유도했지요.
저자들은 이 한계를 극복하기 위해 비슷한 local condition을 가지는 네 가지 초기화 분포 p(θ₀)에 집중하며 실험을 진행합니다.
- Random initialization: Xavier, He 등 랜덤 초기화 분포에서 여러 θ₀ 샘플링
- Fixed initialization: 특정 랜덤 초기화 하나를 고정
- Random pre-trained weights: 같은 데이터셋으로 학습된 여러 pre-trained 모델 샘플링
- Fixed pre-trained weights: 특정 pre-trained 모델 하나를 고정
여기까지 내용이 길었습니다...
먼저 위의 내용들에 대한 실험 결과 먼저 설명한 후에 나머지 내용들 소개드리겠습니다.
6. Main Experimental Results
MNIST와 CIFAR10에서 이미지 분류 실험을 수행합니다.
MNIST는 LeNet(full 학습 시 99%), CIFAR10은 별도 네트워크(full 학습 시 80%)를 사용합니다.
+ Random Initialization 실험에서는 200개의 홀드아웃 모델에 대한 평균과 표준편차를 보고한다고 합니다.
베이스라인들은 여러 학습률과 에포크 조합 중 가장 좋은 결과를 보고하여 공정한 비교를 보장합니다.
- Random real images: 카테고리당 같은 수의 실제 이미지를 랜덤 샘플링
- Optimized real images: 여러 랜덤 세트 중 성능 상위 20%를 선택
- k-means: 각 카테고리에서 클러스터 중심을 학습 이미지로 사용
- Average real images: 각 카테고리의 평균 이미지를 계산하여 사용

Fixed initialization 설정에서 MNIST는 10장의 증류 이미지로 12.90%에서 93.76%로, CIFAR10은 100장으로 8.82%에서 54.03%로 성능이 향상됩니다.
왼쪽에 써져 있는 LR은 각 에포크에서 사용되는 optimized learning rate입니다.
이는 소수의 증류 이미지만으로도 데이터셋의 핵심 정보를 압축할 수 있음을 보여주는 대표적인 실험입니다.

Random initialization 설정에서는 여러 Xavier 초기화에 대해 평균적으로 잘 작동하는 증류 이미지를 학습합니다.
논문에서는 특정 초기화에 맞춤화되지 않아 이미지가 더 의미 있게 보이며, 각 클래스의 판별적 특징을 잘 드러낸다고 주장합니다.
여기서는 MNIST는 79.50%, CIFAR10은 36.79%의 정확도를 달성합니다.
Fixed initialization보다 성능은 낮지만, 새로운 랜덤 초기화에도 일반화된다는 장점이 있다고 하네요.

Figure 4a는 스텝 수가 늘어날수록 성능이 크게 향상됨을 보여줍니다.
Figure 4b는 에포크 수에 따라 비슷하지만 더 느린 향상을 보여줍니다.
저자들은 더 많은 에포크로 학습하면 증류 이미지의 지식을 충분히 학습할 수 있지만, 최종 성능은 결국 총 이미지 수에 의해 제한된다고 언급합니다.
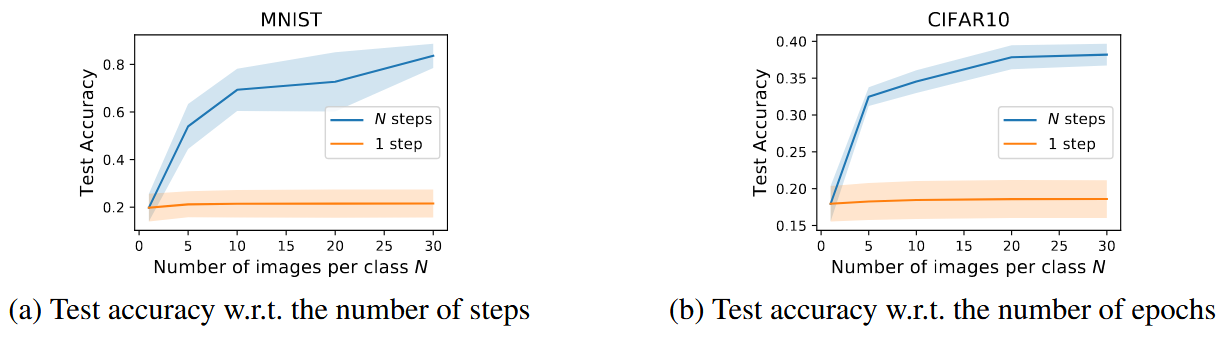
Figure 5는 같은 수의 증류 이미지를 사용할 때, 여러 스텝으로 나누어 학습하는 것이 한 스텝에 모두 사용하는 것보다 훨씬 효과적임을 보여줍니다.
이는 Section 3.3에서 분석한 single-step의 이론적 한계를 실험적으로 확인한 결과라고 할 수 있습니다.

Table 1은 제안 방법과 베이스라인의 성능을 비교하며, CIFAR10, MNIST 데이터셋에서 대부분 베이스라인을 능가하는 결과를 보입니다.
7. Additional Applications

논문에서는 이미지 분류에 국한하지 않고, 두 가지 추가 태스크에서도 dataset distillation의 성능을 실험합니다.
1. Domain Adaptation
한 데이터셋(예: SVHN)으로 학습된 모델을 다른 데이터셋(예: MNIST)에서 잘 작동하도록 적응시키는 것이 Domain Adaptation이죠.
논문에서는 소수의 증류 이미지만으로 이러한 adaptation을 빠르게 수행할 수 있음을 보입니다 (Figure 1b).
2. Malicious Data Poisoning
이 task는 학습 데이터에 악의적인 데이터를 주입하여 모델을 의도적으로 망가뜨리는 공격 기법입니다.
기존 data poisoning은 잘못된 데이터를 학습 데이터에 저장하고 여러 에포크 반복 학습시켜야 했는데, 반면 이 논문의 방식은 distilled images를 사용하면 단 한 번의 경사하강법 스텝만으로 특정 클래스를 오분류하도록 모델을 망가뜨릴 수 있다고 주장합니다.

Table 2는 세 가지 숫자 데이터셋(MNIST, USPS, SVHN) 간의 도메인 적응 성능을 비교합니다.
예를 들어 S→M은 SVHN으로 학습된 모델을 MNIST에 적응시키는 것이지요.
해당 실험에서는 100장의 증류 이미지(10 GD 스텝, 3 에포크)를 사용하며, 제안하는 방법이 기존 few-shot 도메인 적응 방법과 대부분의 베이스라인을 능가하는 결과를 보입니다.

Table 3은 ImageNet으로 사전학습된 AlexNet을 PASCAL-VOC와 CUB-200 데이터셋에 적응시키는 실험입니다.
카테고리당 단 1장의 증류 이미지만 사용하여 베이스라인을 크게 능가하며, 수천 장의 전체 데이터셋으로 fine-tuning한 성능과 거의 대등한 결과를 달성했습니다.
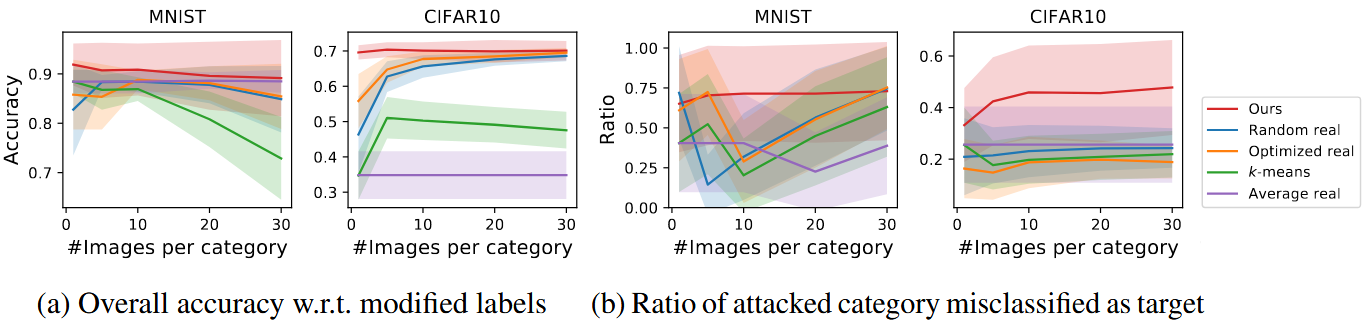
Figure 6은 Data Poisoning 실험 결과입니다.
Figure 6b는 공격 성공률(오분류 비율)을 보여주며, MNIST에서는 베이스라인과 비슷하지만 CIFAR10에서는 제안 방법(빨간색)이 베이스라인을 크게 능가하는 것을 확인하실 수 있습니다.
저자들은 해당 방법론이 정확한 모델 가중치에 접근할 필요 없이 새로운 모델에도 일반화된다고 주장합니다.
본 논문은 대규모 학습 데이터의 지식을 소수의 합성 이미지로 압축하는 dataset distillation을 제안하고, image classification뿐 아니라 domain adaptation과 data poisoning 공격까지 다양한 응용을 보여주었습니다.
8. Conclusion
본 논문은 대규모 학습 데이터의 지식을 소수의 합성 이미지로 압축하는 dataset distillation을 제안하고, image classification뿐 아니라 domain adaptation과 data poisoning 공격까지 다양한 응용을 보여주었습니다.
저자들은 향후 ImageNet 같은 대규모 데이터셋과 오디오, 텍스트 등 다른 데이터 타입으로의 확장을 계획하고 있다고 언급합니다.
확인해보니 Dataset Distillation by Matching Training Trajectories (CVPR 2022) 후속 논문을 내셨더라구요.
관심 있으신 분은 위 논문도 참고하시면 좋을 것 같습니다. 😊
참 길었습니다..
오랜만에 준비해 본 논문 리뷰인데...! 여러분께 큰 도움이 되셨으면 좋겠습니다.
궁금한 점이 있다면 댓글 남겨주세요! 😘
